Calculating the bounding points for the area of a “Pie Segment” and “sub areas”

Question

Background:

I was recently playing around with GDI+ to draw a "Disc" displaying a sweeping color change through 360 degrees. (I dug up some HSL to RGB code to loop through HSL(1,1,1) -> HSL(360,1,1))

Regarding the disc, I first drew a full solid circle using the above, and then a second circle in Grey over the center to give the following

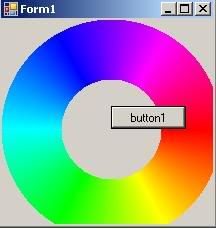
So this is all fine... but I realised that GDI+ is insulating us from a lot of the tricky match that's going on here by way of the FillPie method. Also, FillPie requires you to supply a bounding rectangle for the pie as opposed to a Radius Length. It also does a full segment fill and doesnt allow you to specify a part of that segment only.

Question:

Can anyone point me in the direction of some Math functions or give any explanation on what forumla I would need to calculate the area & plot points of the following "Green Filled Area" given:

Point `c` - an x,y co-ordinate
Angle `A` - an angle from horizontal
Angle `B  - an angle from horizontal where `B` - `A` == the sweep angle
Length `r` - a distance from `c`
Length `r2` - a distance from `c` where `r2` - `r` == the `height` of the segment to be filled.

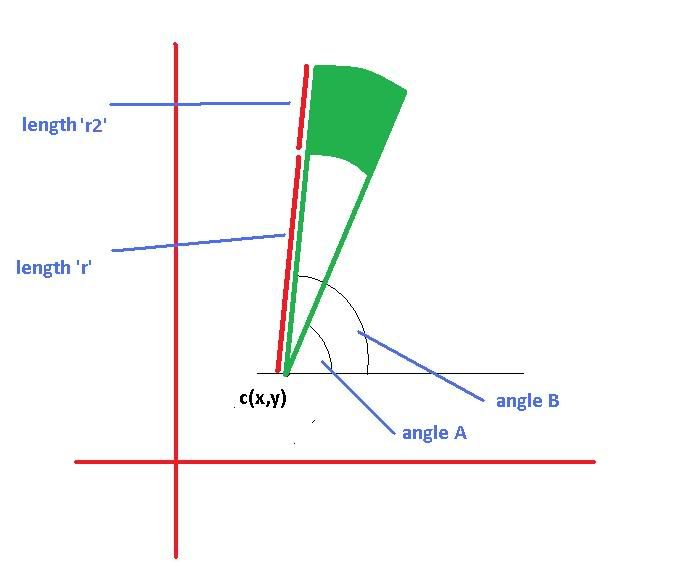
Links to Math sources are fine but I've had a quick google & look at Wolfram Math and could find what I was looking for. Also, if there was some way to generate a sequence of bounding (x,y) co-or's that could be passed as a Point[] to Graphics.FillPolygon, that'd be cool too.

Answer 1

The area is the difference of the outer and inner disc parts. The area of a disc part is proportional to the angle sweep:

area = (b-a)*((r+r2)^2-r^2)/2

a and b must be expressed in radians. For b-a = 2*Pi, area = Pi*(r+r2)^2 - Pi*r^2 is the difference of the areas of the outer and inner discs.

You can generate points on the inner / outer circle using

x = cx + r * cos(t)     /     x = cx + (r+r2) * cos(t)
y = cy + r * sin(t)     /     y = cy + (r+r2) * sin(t)

Where t varies from a to b.

Answer 2

Hope this helps. The second part provides a method for calculating the area of a sector of a circle

http://www.wikihow.com/Calculate-the-Area-of-a-Circle

Answer 3

The area of a segment of a circle is simply the angle of the arc (in radians) times the radius. So the area of the green circle is obviously:

(B-A) * r2

Answer 4

You need to draw lines (this pseudo code):

for aa from A to B
  set color to required color // you could use aa in an equation with HSL to get something like your sample
  x1=r*cos(aa)+x
  y1=r*sin(aa)+y
  x2=r1*cos(aa)+x
  y2=r1*sin(aa)+y
  draw line between (x1,y1) and (x2,y2)

for a small-enough increment in the angles, and small-enough radii, this should be OK.

The points you're looking for are (x1,y1) and (x2,y2) for each angle aa