What can be the efficient approach to solve the 8 puzzle problem?
Question
The 8-puzzle is a square board with 9 positions, filled by 8 numbered tiles and one gap. At any point, a tile adjacent to the gap can be moved into the gap, creating a new gap position. In other words the gap can be swapped with an adjacent (horizontally and vertically) tile. The objective in the game is to begin with an arbitrary configuration of tiles, and move them so as to get the numbered tiles arranged in ascending order either running around the perimeter of the board or ordered from left to right, with 1 in the top left-hand position.
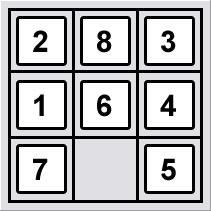
I was wondering what approach will be efficient to solve this problem?
Solution
I will just attempt to rewrite the previous answer with more details on why it is optimal.
The A* algorithm taken directly from wikipedia is
function A*(start,goal)
closedset := the empty set // The set of nodes already evaluated.
openset := set containing the initial node // The set of tentative nodes to be evaluated.
came_from := the empty map // The map of navigated nodes.
g_score[start] := 0 // Distance from start along optimal path.
h_score[start] := heuristic_estimate_of_distance(start, goal)
f_score[start] := h_score[start] // Estimated total distance from start to goal through y.
while openset is not empty
x := the node in openset having the lowest f_score[] value
if x = goal
return reconstruct_path(came_from, came_from[goal])
remove x from openset
add x to closedset
foreach y in neighbor_nodes(x)
if y in closedset
continue
tentative_g_score := g_score[x] + dist_between(x,y)
if y not in openset
add y to openset
tentative_is_better := true
elseif tentative_g_score < g_score[y]
tentative_is_better := true
else
tentative_is_better := false
if tentative_is_better = true
came_from[y] := x
g_score[y] := tentative_g_score
h_score[y] := heuristic_estimate_of_distance(y, goal)
f_score[y] := g_score[y] + h_score[y]
return failure
function reconstruct_path(came_from, current_node)
if came_from[current_node] is set
p = reconstruct_path(came_from, came_from[current_node])
return (p + current_node)
else
return current_node
So let me fill in all the details here.
heuristic_estimate_of_distance is the function Σ d(xi) where d(.) is the Manhattan distance of each square xi from its goal state.
So the setup
1 2 3
4 7 6
8 5
would have a heuristic_estimate_of_distance of 1+2+1=4 since each of 8,5 are one away from their goal position with d(.)=1 and 7 is 2 away from its goal state with d(7)=2.
The set of nodes that the A* searches over is defined to be the starting position followed by all possible legal positions. That is lets say the starting position x is as above:
x =
1 2 3
4 7 6
8 5
then the function neighbor_nodes(x) produces the 2 possible legal moves:
1 2 3
4 7
8 5 6
or
1 2 3
4 7 6
8 5
The function dist_between(x,y) is defined as the number of square moves that took place to transition from state x to y. This is mostly going to be equal to 1 in A* always for the purposes of your algorithm.
closedset and openset are both specific to the A* algorithm and can be implemented using standard data structures (priority queues I believe.) came_from is a data structure used
to reconstruct the solution found using the function reconstruct_path who's details can be found on wikipedia. If you do not wish to remember the solution you do not need to implement this.
Last, I will address the issue of optimality. Consider the excerpt from the A* wikipedia article:
"If the heuristic function h is admissible, meaning that it never overestimates the actual minimal cost of reaching the goal, then A* is itself admissible (or optimal) if we do not use a closed set. If a closed set is used, then h must also be monotonic (or consistent) for A* to be optimal. This means that for any pair of adjacent nodes x and y, where d(x,y) denotes the length of the edge between them, we must have: h(x) <= d(x,y) +h(y)"
So it suffices to show that our heuristic is admissible and monotonic. For the former (admissibility), note that given any configuration our heuristic (sum of all distances) estimates that each square is not constrained by only legal moves and can move freely towards its goal position, which is clearly an optimistic estimate, hence our heuristic is admissible (or it never over-estimates since reaching a goal position will always take at least as many moves as the heuristic estimates.)
The monotonicity requirement stated in words is: "The heuristic cost (estimated distance to goal state) of any node must be less than or equal to the cost of transitioning to any adjacent node plus the heuristic cost of that node."
It is mainly to prevent the possibility of negative cycles, where transitioning to an unrelated node may decrease the distance to the goal node more than the cost of actually making the transition, suggesting a poor heuristic.
To show monotonicity its pretty simple in our case. Any adjacent nodes x,y have d(x,y)=1 by our definition of d. Thus we need to show
h(x) <= h(y) + 1
which is equivalent to
h(x) - h(y) <= 1
which is equivalent to
Σ d(xi) - Σ d(yi) <= 1
which is equivalent to
Σ d(xi) - d(yi) <= 1
We know by our definition of neighbor_nodes(x) that two neighbour nodes x,y can have at most the position of one square differing, meaning that in our sums the term
d(xi) - d(yi) = 0
for all but 1 value of i. Lets say without loss of generality this is true of i=k. Furthermore, we know that for i=k, the node has moved at most one place, so its distance to a goal state must be at most one more than in the previous state thus:
Σ d(xi) - d(yi) = d(xk) - d(yk) <= 1
showing monotonicity. This shows what needed to be showed, thus proving this algorithm will be optimal (in a big-O notation or asymptotic kind of way.)
Note, that I have shown optimality in terms of big-O notation but there is still lots of room to play in terms of tweaking the heuristic. You can add additional twists to it so that it is a closer estimate of the actual distance to the goal state, however you have to make sure that the heuristic is always an underestimate otherwise you loose optimality!
EDIT MANY MOONS LATER
Reading this over again (much) later, I realized the way I wrote it sort of confounds the meaning of optimality of this algorithm.
There are two distinct meanings of optimality I was trying to get at here:
1) The algorithm produces an optimal solution, that is the best possible solution given the objective criteria.
2) The algorithm expands the least number of state nodes of all possible algorithms using the same heuristic.
The simplest way to understand why you need admissibility and monotonicity of the heuristic to obtain 1) is to view A* as an application of Dijkstra's shortest path algorithm on a graph where the edge weights are given by the node distance traveled thus far plus the heuristic distance. Without these two properties, we would have negative edges in the graph, thereby negative cycles would be possible and Dijkstra's shortest path algorithm would no longer return the correct answer! (Construct a simple example of this to convince yourself.)
2) is actually quite confusing to understand. To fully understand the meaning of this, there are a lot of quantifiers on this statement, such as when talking about other algorithms, one refers to similar algorithms as A* that expand nodes and search without a-priori information (other than the heuristic.) Obviously, one can construct a trivial counter-example otherwise, such as an oracle or genie that tells you the answer at every step of the way. To understand this statement in depth I highly suggest reading the last paragraph in the History section on Wikipedia as well as looking into all the citations and footnotes in that carefully stated sentence.
I hope this clears up any remaining confusion among would-be readers.
OTHER TIPS
You can use the heuristic that is based on the positions of the numbers, that is the higher the overall sum of all the distances of each letter from its goal state is, the higher the heuristic value. Then you can implement A* search which can be proved to be the optimal search in terms of time and space complexity (provided the heuristic is monotonic and admissible.) http://en.wikipedia.org/wiki/A*_search_algorithm
Since the OP cannot post a picture, this is what he's talking about:
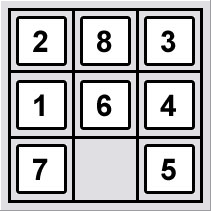
As far as solving this puzzle, goes, take a look at the iterative deepening depth-first search algorithm, as made relevant to the 8-puzzle problem by this page.
Donut's got it! IDDFS will do the trick, considering the relatively limited search space of this puzzle. It would be efficient hence respond to the OP's question. It would find the optimal solution, but not necessarily in optimal complexity.
Implementing IDDFS would be the more complicated part of this problem, I just want to suggest an simple approach to managing the board, the games rules etc. This in particular addresses a way to obtain initial states for the puzzle which are solvable. An hinted in the notes of the question, not all random assignemts of 9 tites (considering the empty slot a special tile), will yield a solvable puzzle. It is a matter of mathematical parity... So, here's a suggestions to model the game:
Make the list of all 3x3 permutation matrices which represent valid "moves" of the game. Such list is a subset of 3x3s w/ all zeros and two ones. Each matrix gets an ID which will be quite convenient to keep track of the moves, in the IDDFS search tree. An alternative to matrices, is to have two-tuples of the tile position numbers to swap, this may lead to faster implementation.
Such matrices can be used to create the initial puzzle state, starting with the "win" state, and running a arbitrary number of permutations selected at random. In addition to ensuring that the initial state is solvable this approach also provides a indicative number of moves with which a given puzzle can be solved.
Now let's just implement the IDDFS algo and [joke]return the assignement for an A+[/joke]...
This is an example of the classical shortest path algorithm. You can read more about shortest path here and here.
In short, think of all possible states of the puzzle as of vertices in some graph. With each move you change states - so, each valid move represents an edge of the graph. Since moves don't have any cost, you may think of the cost of each move being 1. The following c++-like pseudo-code will work for this problem:
{
int[][] field = new int[3][3];
// fill the input here
map<string, int> path;
queue<string> q;
put(field, 0); // we can get to the starting position in 0 turns
while (!q.empty()) {
string v = q.poll();
int[][] take = decode(v);
int time = path.get(v);
if (isFinalPosition(take)) {
return time;
}
for each valid move from take to int[][] newPosition {
put(newPosition, time + 1);
}
}
// no path
return -1;
}
void isFinalPosition(int[][] q) {
return encode(q) == "123456780"; // 0 represents empty space
}
void put(int[][] position, int time) {
string s = encode(newPosition);
if (!path.contains(s)) {
path.put(s, time);
}
}
string encode(int[][] field) {
string s = "";
for (int i = 0; i < 3; i++) for (int j = 0; j < 3; j++) s += field[i][j];
return s;
}
int[][] decode(string s) {
int[][] ans = new int[3][3];
for (int i = 0; i < 3; i++) for (int j = 0; j < 3; j++) field[i][j] = s[i * 3 + j];
return ans;
}
See this link for my parallel iterative deepening search for a solution to the 15-puzzle, which is the 4x4 big-brother of the 8-puzzle.