Trova i percorsi tra due nodi dato?
-
23-08-2019 - |
Domanda
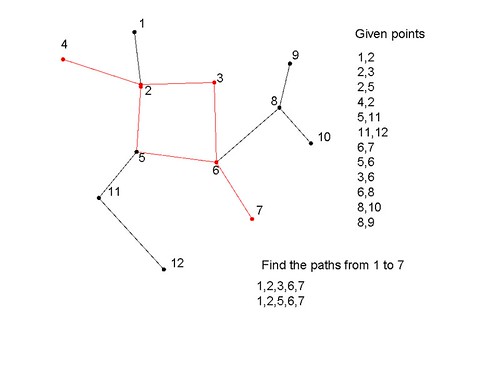
Dire che ho nodi collegati al modo di seguito, come faccio arrivare al numero di percorsi che esistono tra i punti dato, e dettagli del percorso?
1,2 //node 1 and 2 are connected
2,3
2,5
4,2
5,11
11,12
6,7
5,6
3,6
6,8
8,10
8,9
Trova i percorsi da 1 a 7:
Risposta: 2 percorsi trovati e sono
1,2,3,6,7
1,2,5,6,7
qui è bello Ho intenzione di utilizzare lo stesso
Ecco il frammento dal link qui sopra in Python
# a sample graph
graph = {'A': ['B', 'C','E'],
'B': ['A','C', 'D'],
'C': ['D'],
'D': ['C'],
'E': ['F','D'],
'F': ['C']}
class MyQUEUE: # just an implementation of a queue
def __init__(self):
self.holder = []
def enqueue(self,val):
self.holder.append(val)
def dequeue(self):
val = None
try:
val = self.holder[0]
if len(self.holder) == 1:
self.holder = []
else:
self.holder = self.holder[1:]
except:
pass
return val
def IsEmpty(self):
result = False
if len(self.holder) == 0:
result = True
return result
path_queue = MyQUEUE() # now we make a queue
def BFS(graph,start,end,q):
temp_path = [start]
q.enqueue(temp_path)
while q.IsEmpty() == False:
tmp_path = q.dequeue()
last_node = tmp_path[len(tmp_path)-1]
print tmp_path
if last_node == end:
print "VALID_PATH : ",tmp_path
for link_node in graph[last_node]:
if link_node not in tmp_path:
#new_path = []
new_path = tmp_path + [link_node]
q.enqueue(new_path)
BFS(graph,"A","D",path_queue)
-------------results-------------------
['A']
['A', 'B']
['A', 'C']
['A', 'E']
['A', 'B', 'C']
['A', 'B', 'D']
VALID_PATH : ['A', 'B', 'D']
['A', 'C', 'D']
VALID_PATH : ['A', 'C', 'D']
['A', 'E', 'F']
['A', 'E', 'D']
VALID_PATH : ['A', 'E', 'D']
['A', 'B', 'C', 'D']
VALID_PATH : ['A', 'B', 'C', 'D']
['A', 'E', 'F', 'C']
['A', 'E', 'F', 'C', 'D']
VALID_PATH : ['A', 'E', 'F', 'C', 'D']
Soluzione
Larghezza-prima ricerca attraversa un grafico e infatti trova tutti i percorsi da un punto di partenza nodo. Di solito, BFS non tenere tutti i percorsi, tuttavia. Invece, si aggiorna una funzione prededecessor π per salvare il percorso più breve. Si può facilmente modificare l'algoritmo in modo che π(n) non solo negozio di una predecessore, ma un elenco di possibili predecessori.
Poi tutti i percorsi possibili sono codificati in questa funzione, e attraversando π ricorsivamente ottenere tutte le possibili combinazioni di percorso.
Un buon pseudocodice che usa questa notazione può essere trovato in Introduzione agli algoritmi di Cormen et al. e successivamente è stato utilizzato in molti script universitari sul tema. Una ricerca su Google per “BFS pseudocode predecessore π” sradica questo colpo su Pila Scambio .
Altri suggerimenti
Per chi non è esperto di Python, lo stesso codice in C ++
//@Author :Ritesh Kumar Gupta
#include <stdio.h>
#include <vector>
#include <algorithm>
#include <vector>
#include <queue>
#include <iostream>
using namespace std;
vector<vector<int> >GRAPH(100);
inline void print_path(vector<int>path)
{
cout<<"[ ";
for(int i=0;i<path.size();++i)
{
cout<<path[i]<<" ";
}
cout<<"]"<<endl;
}
bool isadjacency_node_not_present_in_current_path(int node,vector<int>path)
{
for(int i=0;i<path.size();++i)
{
if(path[i]==node)
return false;
}
return true;
}
int findpaths(int source ,int target ,int totalnode,int totaledge )
{
vector<int>path;
path.push_back(source);
queue<vector<int> >q;
q.push(path);
while(!q.empty())
{
path=q.front();
q.pop();
int last_nodeof_path=path[path.size()-1];
if(last_nodeof_path==target)
{
cout<<"The Required path is:: ";
print_path(path);
}
else
{
print_path(path);
}
for(int i=0;i<GRAPH[last_nodeof_path].size();++i)
{
if(isadjacency_node_not_present_in_current_path(GRAPH[last_nodeof_path][i],path))
{
vector<int>new_path(path.begin(),path.end());
new_path.push_back(GRAPH[last_nodeof_path][i]);
q.push(new_path);
}
}
}
return 1;
}
int main()
{
//freopen("out.txt","w",stdout);
int T,N,M,u,v,source,target;
scanf("%d",&T);
while(T--)
{
printf("Enter Total Nodes & Total Edges\n");
scanf("%d%d",&N,&M);
for(int i=1;i<=M;++i)
{
scanf("%d%d",&u,&v);
GRAPH[u].push_back(v);
}
printf("(Source, target)\n");
scanf("%d%d",&source,&target);
findpaths(source,target,N,M);
}
//system("pause");
return 0;
}
/*
Input::
1
6 11
1 2
1 3
1 5
2 1
2 3
2 4
3 4
4 3
5 6
5 4
6 3
1 4
output:
[ 1 ]
[ 1 2 ]
[ 1 3 ]
[ 1 5 ]
[ 1 2 3 ]
The Required path is:: [ 1 2 4 ]
The Required path is:: [ 1 3 4 ]
[ 1 5 6 ]
The Required path is:: [ 1 5 4 ]
The Required path is:: [ 1 2 3 4 ]
[ 1 2 4 3 ]
[ 1 5 6 3 ]
[ 1 5 4 3 ]
The Required path is:: [ 1 5 6 3 4 ]
*/
l'algoritmo di Dijkstra si applica più ai percorsi ponderati e suona come il manifesto mancava di trovare tutti i percorsi, non solo il più breve.
Per questa applicazione, mi piacerebbe costruire un grafico (l'applicazione suona come esso non avrebbe bisogno di essere diretto) e utilizzare il metodo di ricerca preferito. Sembra che si desidera che tutti i percorsi, non solo una supposizione al più breve, in modo da utilizzare un semplice algoritmo ricorsivo di vostra scelta.
L'unico problema è se il grafico può essere ciclico.
Con i collegamenti:
- 1, 2
- 1, 3
- 2, 3
- 2, 4
Mentre alla ricerca di un percorso da 1-> 4, si potrebbe avere un ciclo di 1 -> 2 -> 3 -.> 1
In questo caso, allora io terrei una pila come l'attraversamento dei nodi. Ecco una lista con i passaggi per questo grafico e lo stack risultante (scusate per la formattazione - senza opzione di tabella):
nodo corrente (possibili prossimi nodi meno da dove veniamo) [pila]
- 1 (2, 3) [1]
- 2 (3, 4) [1, 2]
- 3 (1) [1, 2, 3]
- 1 (2, 3) [1, 2, 3, 1] // errore - duplicato numero sullo stack - ciclo rilevato
- 3 () [1, 2, 3] // back-intensificato al nodo tre e spuntato 1 dallo stack. Niente più nodi da esplorare da qui
- 2 (4) [1, 2] // back-intensificato al nodo 2 e spuntato 1 dallo stack.
- 4 () [1, 2, 4] // nodo Bersaglio trovato - pila record per un percorso. Niente più nodi da esplorare da qui
- 2 () [1, 2] // back-intensificato al nodo 2 e 4 spuntato dallo stack. Niente più nodi da esplorare da qui
- 1 (3) [1] // back-intensificato al nodo 1 e 2 spuntato dallo stack.
- 3 (2) [1, 3]
- 2 (1, 4) [1, 3, 2]
- 1 (2, 3) [1, 3, 2, 1] // errore - duplicato numero sullo stack - ciclo rilevato
- 2 (4) [1, 3, 2] // back-intensificato al nodo 2 e spuntato 1 dallo stack
- 4 () [1, 3, 2, 4] nodo Bersaglio trovato - pila record per un percorso. Niente più nodi da esplorare da qui
- 2 () [1, 3, 2] // back-intensificato al nodo 2 e 4 spuntato dallo stack. Niente più nodi
- 3 () [1, 3] // back-intensificato al nodo 3 e spuntato 2 dallo stack. Niente più nodi
- 1 () [1] // back-intensificato al nodo 1 e 3 spuntato dallo stack. Niente più nodi
- Fatto con 2 tracciati registrati di [1, 2, 4] e [1, 3, 2, 4]
Il codice originale è un po 'ingombrante e si potrebbe desiderare di utilizzare la collections.deque, invece, se si desidera utilizzare BFS da trovare se esiste un percorso tra 2 punti sul grafico. Ecco una soluzione rapida ho inciso su:
Nota: questo metodo potrebbe continuare all'infinito se esiste alcun percorso tra i due nodi. Non ho ancora testato tutti i casi, YMMV.
from collections import deque
# a sample graph
graph = {'A': ['B', 'C','E'],
'B': ['A','C', 'D'],
'C': ['D'],
'D': ['C'],
'E': ['F','D'],
'F': ['C']}
def BFS(start, end):
""" Method to determine if a pair of vertices are connected using BFS
Args:
start, end: vertices for the traversal.
Returns:
[start, v1, v2, ... end]
"""
path = []
q = deque()
q.append(start)
while len(q):
tmp_vertex = q.popleft()
if tmp_vertex not in path:
path.append(tmp_vertex)
if tmp_vertex == end:
return path
for vertex in graph[tmp_vertex]:
if vertex not in path:
q.append(vertex)
In Prolog (in particolare, SWI-Prolog)
:- use_module(library(tabling)).
% path(+Graph,?Source,?Target,?Path)
:- table path/4.
path(_,N,N,[N]).
path(G,S,T,[S|Path]) :-
dif(S,T),
member(S-I, G), % directed graph
path(G,I,T,Path).
Test:
paths :- Graph =
[ 1- 2 % node 1 and 2 are connected
, 2- 3
, 2- 5
, 4- 2
, 5-11
,11-12
, 6- 7
, 5- 6
, 3- 6
, 6- 8
, 8-10
, 8- 9
],
findall(Path, path(Graph,1,7,Path), Paths),
maplist(writeln, Paths).
?- paths.
[1,2,3,6,7]
[1,2,5,6,7]
true.
Se si desidera che tutti i percorsi, l'uso ricorsione.
L'utilizzo di un lista di adiacenza, di preferenza, creare una funzione f () che tenta di compilare un elenco aggiornato dei vertici visitati. In questo modo:
void allPaths(vector<int> previous, int current, int destination)
{
previous.push_back(current);
if (current == destination)
//output all elements of previous, and return
for (int i = 0; i < neighbors[current].size(); i++)
allPaths(previous, neighbors[current][i], destination);
}
int main()
{
//...input
allPaths(vector<int>(), start, end);
}
A causa del fatto che il vettore viene passato per valore (e quindi eventuali modifiche apportate più in basso nella procedura ricorsiva non sono permanenti), tutte le combinazioni possibili sono enumerati.
È possibile ottenere un po 'di efficienza facendo passare il precedente vettore per riferimento (e quindi non hanno bisogno di copiare il vettore più e più volte), ma si dovrà fare in modo che le cose si fanno popped_back () manualmente.
Ancora una cosa: se il grafico ha cicli, questo non funzionerà. (Suppongo in questo caso si vorrà trovare tutti semplici percorsi, quindi) Prima di aggiungere qualcosa in precedente vettore, prima verifica se è già in là.
Se si desidera che tutti i più brevi percorsi, utilizzare il suggerimento di Konrad con questo algoritmo.
data la matrice di adiacenza:
{0, 1, 3, 4, 0, 0}
{0, 0, 2, 1, 2, 0}
{0, 1, 0, 3, 0, 0}
{0, 1, 1, 0, 0, 1}
{0, 0, 0, 0, 0, 6}
{0, 1, 0, 1, 0, 0}
il seguente codice di Wolfram Mathematica risolve il problema di trovare tutti i semplici percorsi tra due nodi di un grafo. Ho usato semplice ricorsione, e due var globale per tenere traccia dei cicli e per memorizzare l'uscita desiderata. il codice non è stato ottimizzato solo per motivi di chiarezza codice. la "stampa" dovrebbe essere utile per chiarire come funziona.
cycleQ[l_]:=If[Length[DeleteDuplicates[l]] == Length[l], False, True];
getNode[matrix_, node_]:=Complement[Range[Length[matrix]],Flatten[Position[matrix[[node]], 0]]];
builtTree[node_, matrix_]:=Block[{nodes, posAndNodes, root, pos},
If[{node} != {} && node != endNode ,
root = node;
nodes = getNode[matrix, node];
(*Print["root:",root,"---nodes:",nodes];*)
AppendTo[lcycle, Flatten[{root, nodes}]];
If[cycleQ[lcycle] == True,
lcycle = Most[lcycle]; appendToTree[root, nodes];,
Print["paths: ", tree, "\n", "root:", root, "---nodes:",nodes];
appendToTree[root, nodes];
];
];
appendToTree[root_, nodes_] := Block[{pos, toAdd},
pos = Flatten[Position[tree[[All, -1]], root]];
For[i = 1, i <= Length[pos], i++,
toAdd = Flatten[Thread[{tree[[pos[[i]]]], {#}}]] & /@ nodes;
(* check cycles!*)
If[cycleQ[#] != True, AppendTo[tree, #]] & /@ toAdd;
];
tree = Delete[tree, {#} & /@ pos];
builtTree[#, matrix] & /@ Union[tree[[All, -1]]];
];
];
per chiamare il codice: initNode = 1; endNode = 6; lcycle = {}; albero = {{initNode}}; builtTree [initNode, matrice];
percorsi: {{1}} root: 1 --- nodi: {2,3,4}
percorsi: {{1,2}, {1,3}, {1,4}} root: 2 --- nodi: {3,4,5}
percorsi: {{1,3}, {1,4}, {1,2,3}, {1,2,4}, {1,2,5}} radice: 3 --- nodi: {2,4}
percorsi: {{1,4}, {1,2,4}, {1,2,5}, {1,3,4}, {1,2,3,4}, {1,3 , 2,4}, {1,3,2,5}} root: 4 --- nodi: {2,3,6}
percorsi: {{1,2,5}, {1,3,2,5}, {1,4,6}, {1,2,4,6}, {1,3,4,6 }, {1,2,3,4,6}, {1,3,2,4,6}, {1,4,2,5}, {1,3,4,2,5}, {1 , 4,3,2,5}} nodi 5 ---:: radice {6}
RISULTATI: {{1, 4, 6}, {1, 2, 4, 6}, {1, 2, 5, 6}, {1, 3, 4, 6}, {1, 2, 3 , 4, 6}, {1, 3, 2, 4, 6}, {1, 3, 2, 5, 6}, {1, 4, 2, 5, 6}, {1, 3, 4, 2 , 5, 6}, {1, 4, 3, 2, 5, 6}}
... Purtroppo non posso caricare le immagini per mostrare i risultati in un modo migliore: (
Quello che stai cercando di fare è essenzialmente quello di trovare un percorso tra due vertici in un (regia?) Grafico controllare L'algoritmo di Dijkstra se avete bisogno di più breve percorso o scrivere una semplice funzione ricorsiva se avete bisogno di qualunque cosa esistono percorsi.