Combinatorics Counting Puzzle：ロール20、8面のサイコロ、同じ値の少なくとも5つのサイコロを得る確率

StackOverflow https://stackoverflow.com/questions/1202343

質問

1つのロール20、8面のサイコロ、合計8 ^ 20の可能な結果のゲームを想定します。特定のイベントが発生する確率を計算するために、イベントが発生する可能性のある数を8 ^ 20で除算します。

値3の正確に5つのサイコロを得る方法の数を計算できます（20を選択5）3の注文数を与えます。7^ 15は値3を得ることができない方法の数を与えます15ロール分。

number of ways to get exactly 5, 3's = (20 choose 5)*7^15.

答えは、文字列3,3,3,3,3,0,0,0,0,0,0,0,0,0,0,0を再配置できる方法としても表示できます。 0,0,0,0（20は5を選択）にゼロの値の合計数（7つの正当な値を想定）7 ^ 15（これは正しい）。

  • 質問1：同じ値のサイコロを正確に5つ取得する方法の数を計算するには（つまり、すべてのダイの値について）。 注：上記の最初の回答を単純に使用してbt 8を乗算すると、膨大な量の二重カウントが発生しますか？

    各ケース（5 1's）、（5、2's）、（5、3's）、...（5's、8）を解決できることを理解しています（より単純に8 *（5 1's） ）。次に、重複数（5 1's）と（5 2's）、（5 1's）と（5 3's）...（5 1's）と（5、2's）と...と（5、8's）の合計を減算しますしかし、これは非常に面倒です。これを一般化して、多数のサンプルと多数のクラスにスケールアップします。

  • 同じ値のサイコロを少なくとも 5個取得する方法の数を計算するにはどうすればよいですか

    したがって111110000000000000000または11110100000000000002または11111100000001110000または11011211222222223333であり、00001111222233334444または000511512252363347744ではありません。

数学を説明するか、これをサポートするライブラリ（esp pythonモジュール）を指す回答を探しています。詳細と例の追加ポイント。

役に立ちましたか？

解決

二重カウントは、 Inclusion / Exclusion Principle

次のようになります：

Choose(8,1)*P(one set of 5 Xs) 
- Choose(8,2)*P(a set of 5 Xs and a set of 5 Ys) 
+ Choose(8,3)*P(5 Xs, 5 Ys, 5 Zs) 
- Choose(8,4)*P(5 Xs, 5 Ys, 5 Zs, 5 As)

P(set of 5 Xs) = 20 Choose 5 * 7^15 / 8^20
P(5 Xs, 5 Ys) = 20 Choose 5,5 * 6^10 / 8^20

など。これは、5、6、7..20に適用した結果を単純に合計したかのように、「同じ5つ以上」の問題を直接解決しません。たとえば、10個の1と5個の8があるケースを過剰にカウントします。

2番目の答えを思い付くには、おそらく包含除外を再度適用できます。したがって、P（少なくとも5）= P（20の1セット）+ ... +（P（15の1セット）-7 * P（5ダイスから5のセット））+（（P（1セット14）-7 * P（6から5の1セット）-7 * P（6から6の1セット））。そのためのソースコードを考え出すこと自体がより困難であることが証明されています。

他のヒント

少し時間をかけてモンテカルロシミュレーションを作成し、数学を手作業で計算しながら実行することをお勧めします。数学を終える前にモンテカルロシミュレーションが収束し、ソリューションを確認できることを願っています。

少し高速なオプションには、数学の質問用のSOクローンの作成が含まれる場合があります。

i個のs-sidedダイスの合計の正確な確率分布Fs、iは、シングルダイ確率分布とそれ自体の反復畳み込みとして計算できます。

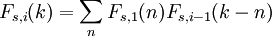
alt text

where 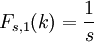alt textすべての alt text およびその他の場合は0。

http://en.wikipedia.org/wiki/Dice

この問題は、一般化する必要がある場合は非常に困難です（正確な式を取得します）。

しかし、とにかく、アルゴリズムについて説明させてください。 知りたい場合

  

正確に5つを取得する方法の数   同じ値のサイコロ

次のように、前の問題を言い換える必要があります

  

取得する方法の数を計算する   値3のちょうど5つのサイコロ   他の値は正確に5回繰り返すことができます   回

簡単にするために、関数F（20,8,5）（5サイコロ、すべての値）を最初の答え、F（20,8,5,3）（5サイコロ、値3）を2番目の答えとします。 F（20,8,5）= F（20,8,5,3）* 8 + （複数の値が5回繰り返されるイベント）

したがって、F（20,8,5,3）を取得できれば、かなり単純なはずです。 まあ...そんなにない...

まず、いくつかの変数を定義しましょう。 X1、X2、X3 ...、Xi、ここでXi =サイコロを取得する回数i

その後：

F(20,8,5)/20^8 = P(X1=5 or X2=5 or ... or X8=5, with R=20(rolls) and N=8(dice number))

、P（statement）は確率を記述する標準的な方法です。

続行：

F(20,8,5,3)/20^8 = P(X3=5 and X1<>5 and ... and X8<>5, R=20, N=8) 
F(20,8,5,3)/20^8 = 1 - P(X1=5 or X2=5 or X4=5 or X5=5 or X6=5 or X7=5 or X8=5, R=15, N=7)  
F(20,8,5,3)/20^8 = 1 - F(15,7,5)/7^15

再帰的に：

F(15,8,5) = F(15,7,5,1) * 7  
P(X1=5 or X2=5 or X4=5 or X5=5 or X6=5 or X7=5 or X8=5, R=15, N=7) = P(X1=5 and X2<>5 and X4<>5 and .. and X8<>5. R=15, N=7) * 7

F(15,7,5,1)/7^15 = 1 - F(10,6,5)/6^10 F(10,6,5) = F(10,6,5,2) * 6

F(10,6,5,2)/6^10 = 1 - F(5,5,5)/5^5
F(5,5,5) = F(5,5,5,4) * 5

Well then ... F（5,5,5,4）は、他のサイコロが5回繰り返されないなど、5つのロールで値4の5つのサイコロを取得する方法の数です。合計5 ^ 5のうち、たった1つの方法があります。確率は1/5 ^ 5です。

F（5,5,5）は、5つのロールで任意の値（5つの値のうち）の5つのサイコロを取得する方法の数です。明らかに5です。その場合、確率は5/5 ^ 5 = 1/5 ^ 4です。

F（10,6,5,2）は、10回のロールで値2の5つのサイコロを取得する方法の数です。他のサイコロは5回繰り返されません。 F（10,6,5,2）=（1-F（5,5,5）/ 5 ^ 5）* 6 ^ 10 =（1-1 / 5 ^ 4）* 6 ^ 10

まあ...ある部分で間違っているかもしれないと思うが、とにかく、あなたはアイデアを得る。アルゴリズムを理解できるようにしたいと思います。

編集： いくつかのチェックを行いましたが、正確に5回繰り返される複数の値を取得する場合、いくつかのケースを追加する必要があることに気付きました。その部分を解決する時間がありません...

これは私が考えていることです...

サイコロが5個だけだった場合、必要なものを入手するには8つの方法しかありません。

これらの8つの方法のそれぞれについて、他の15のダイスのすべての可能な組み合わせが機能します。

だから-答えは：（8 * 8 15）/ 8 20

（少なくとも5つの答えは同じです。）

n個のイベントでx回発生する式を次のように使用できると思います：

P =確率^ n *（n！/（（n-x）！x！））

したがって、最終結果は0からnまでの結果の合計になります。

これを簡単な方法で1つのステップにまとめて、面倒なものを減らす方法は実際にはありません。この方法を使用すると、コードにも式が記述されます。ただし、独自の階乗法を記述する必要があります。

  float calculateProbability(int tosses, int atLeastNumber) {
    float atLeastProbability = 0;
    float eventProbability = Math.pow( 1.0/8.0, tosses);
    int nFactorial = factorial(tosses);

    for ( i = 1; i <= atLeastNumber; i++) {
      atLeastProbability += eventProbability * (nFactorial / (factorial(tosses - i) * factorial(i) );
    }
  }

再帰的ソリューション：

Prob_same_value(n) = Prob_same_value(n-1) * (1 - Prob_noone_rolling_that_value(N-(n-1)))
ライセンス： CC-BY-SA と 帰属
所属していません StackOverflow
scroll top