Combinatorics Counting Puzzle: Roll 20, 8-sided dice, what is the probability of getting at least 5 dice of the same value

Question

Assume a game in which one rolls 20, 8-sided die, for a total number of 8^20 possible outcomes. To calculate the probability of a particular event occurring, we divide the number of ways that event can occur by 8^20.

One can calculate the number of ways to get exactly 5 dice of the value 3. (20 choose 5) gives us the number of orders of 3. 7^15 gives us the number of ways we can not get the value 3 for 15 rolls.

number of ways to get exactly 5, 3's = (20 choose 5)*7^15.

The answer can also be viewed as how many ways can I rearrange the string 3,3,3,3,3,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0 (20 choose 5) times the total number of values we the zero's (assuming 7 legal values) 7^15 (is this correct).

• Question 1: How can I calculate the number of ways to get exactly 5 dice of the same value(That is, for all die values). Note: if I just naively use my first answer above and multiply bt 8, I get an enormous amount of double counting?

  I understand that I could solve for each of the cases (5 1's), (5, 2's), (5, 3's), ... (5's, 8) sum them (more simply 8*(5 1's) ). Then subtract the sum of number of overlaps (5 1's) and (5 2's), (5 1's) and (5 3's)... (5 1's) and (5, 2's) and ... and (5, 8's) but this seems exceedingly messy. I would a generalization of this in a way that scales up to large numbers of samples and large numbers of classes.

• How can I calculate the number of ways to get at least 5 dice of the same value?

  So 111110000000000000000 or 11110100000000000002 or 11111100000001110000 or 11011211222222223333, but not 00001111222233334444 or 000511512252363347744.

I'm looking for answers which either explain the math or point to a library which supports this (esp python modules). Extra points for detail and examples.

Answer 1

Double counting can be solved by use of the Inclusion/Exclusion Principle

I suspect it comes out to:

Choose(8,1)*P(one set of 5 Xs) 
- Choose(8,2)*P(a set of 5 Xs and a set of 5 Ys) 
+ Choose(8,3)*P(5 Xs, 5 Ys, 5 Zs) 
- Choose(8,4)*P(5 Xs, 5 Ys, 5 Zs, 5 As)

P(set of 5 Xs) = 20 Choose 5 * 7^15 / 8^20
P(5 Xs, 5 Ys) = 20 Choose 5,5 * 6^10 / 8^20

And so on. This doesn't solve the problem directly of 'more then 5 of the same', as if you simply summed the results of this applied to 5,6,7..20; you would over count the cases where you have, say, 10 1's and 5 8's.

You could probably apply inclusion exclusion again to come up with that second answer; so, P(of at least 5)=P(one set of 20)+ ... + (P(one set of 15) - 7*P(set of 5 from 5 dice)) + ((P(one set of 14) - 7*P(one set of 5 from 6) - 7*P(one set of 6 from 6)). Coming up with the source code for that is proving itself more difficult.

Answer 2

I suggest that you spend a little bit of time writing up a Monte Carlo simulation and let it run while you work out the math by hand. Hopefully the Monte Carlo simulation will converge before you're finished with the math and you'll be able to check your solution.

A slightly faster option might involve creating a SO clone for math questions.

Answer 3

The exact probability distribution Fs,i of a sum of i s-sided dice can be calculated as the repeated convolution of the single-die probability distribution with itself.

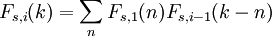
where 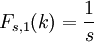for all and 0 otherwise.

http://en.wikipedia.org/wiki/Dice

Answer 4

This problem is really hard if you have to generalize it (get the exact formula).

But anyways, let me explain the algorithm. If you want to know

the number of ways to get exactly 5 dice of the same value

you have to rephrase your previous problem, as

calculate the number of ways to get exactly 5 dice of the value 3 AND no other value can be repeated exactly 5 times

For simplicity's sake, let's call function F(20,8,5) (5 dice, all values) the first answer, and F(20,8,5,3) (5 dice, value 3) the second. We have that F(20,8,5) = F(20,8,5,3) * 8 + (events when more than one value is repeated 5 times)

So if we can get F(20,8,5,3) it should be pretty simple isn't it? Well...not so much...

First, let us define some variables: X1,X2,X3...,Xi , where Xi=number of times we get the dice i

Then:

F(20,8,5)/20^8 = P(X1=5 or X2=5 or ... or X8=5, with R=20(rolls) and N=8(dice number))

, P(statement) being the standard way to write a probability.

we continue:

F(20,8,5,3)/20^8 = P(X3=5 and X1<>5 and ... and X8<>5, R=20, N=8) 
F(20,8,5,3)/20^8 = 1 - P(X1=5 or X2=5 or X4=5 or X5=5 or X6=5 or X7=5 or X8=5, R=15, N=7)  
F(20,8,5,3)/20^8 = 1 - F(15,7,5)/7^15

recursively:

F(15,8,5) = F(15,7,5,1) * 7  
P(X1=5 or X2=5 or X4=5 or X5=5 or X6=5 or X7=5 or X8=5, R=15, N=7) = P(X1=5 and X2<>5 and X4<>5 and .. and X8<>5. R=15, N=7) * 7

---

F(15,7,5,1)/7^15 = 1 - F(10,6,5)/6^10 F(10,6,5) = F(10,6,5,2) * 6

---

F(10,6,5,2)/6^10 = 1 - F(5,5,5)/5^5
F(5,5,5) = F(5,5,5,4) * 5

Well then... F(5,5,5,4) is the number of ways to get 5 dices of value 4 in 5 rolls, such as no other dice repeats 5 times. There is only 1 way, out of a total 5^5. The probability is then 1/5^5.

F(5,5,5) is the number of ways to get 5 dices of any value (out of 5 values) in 5 rolls. It's obviously 5. The probability is then 5/5^5 = 1/5^4.

F(10,6,5,2) is the number of ways to get 5 dices of value 2 in 10 rolls, such as no other dice repeats 5 times. F(10,6,5,2) = (1-F(5,5,5)/5^5) * 6^10 = (1-1/5^4) * 6^10

Well... I think it may be incorrect at some part, but anyway, you get the idea. I hope I could make the algorithm understandable.

edit: I did some checks, and I realized you have to add some cases when you get more than one value repeated exactly 5 times. Don't have time to solve that part thou...

Answer 5

Here is what I am thinking...

If you just had 5 dice, you would only have eight ways to get what you want.

For each of those eight ways, all possible combinations of the other 15 dice work.

So - I think the answer is: (8 * 815) / 820

(The answer for at least 5 the same.)

Answer 6

I believe you can use the formula of x occurrences in n events as:

P = probability^n * (n!/((n - x)!x!))

So the final result is going to be the sum of results from 0 to n.

I don't really see any easy way to combine it into one step that would be less messy. With this way you have the formula spelled out in the code as well. You may have to write your own factorial method though.

  float calculateProbability(int tosses, int atLeastNumber) {
    float atLeastProbability = 0;
    float eventProbability = Math.pow( 1.0/8.0, tosses);
    int nFactorial = factorial(tosses);

    for ( i = 1; i <= atLeastNumber; i++) {
      atLeastProbability += eventProbability * (nFactorial / (factorial(tosses - i) * factorial(i) );
    }
  }

Answer 7

Recursive solution:

Prob_same_value(n) = Prob_same_value(n-1) * (1 - Prob_noone_rolling_that_value(N-(n-1)))