XKCD에서 NP- 완성 문제 해결
-
02-07-2019 - |
문제
문제/코믹한 문제 : http://xkcd.com/287/
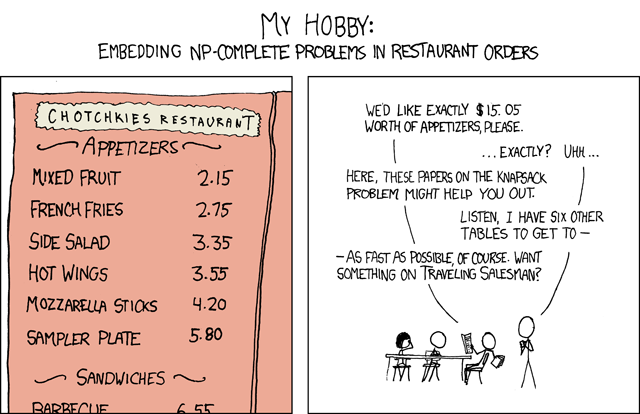
이것이 가장 좋은 방법인지 확실하지 않지만 지금까지 내가 생각해 낸 것이 있습니다. CFML을 사용하고 있지만 누구나 읽을 수 있어야합니다.
<cffunction name="testCombo" returntype="boolean">
<cfargument name="currentCombo" type="string" required="true" />
<cfargument name="currentTotal" type="numeric" required="true" />
<cfargument name="apps" type="array" required="true" />
<cfset var a = 0 />
<cfset var found = false />
<cfloop from="1" to="#arrayLen(arguments.apps)#" index="a">
<cfset arguments.currentCombo = listAppend(arguments.currentCombo, arguments.apps[a].name) />
<cfset arguments.currentTotal = arguments.currentTotal + arguments.apps[a].cost />
<cfif arguments.currentTotal eq 15.05>
<!--- print current combo --->
<cfoutput><strong>#arguments.currentCombo# = 15.05</strong></cfoutput><br />
<cfreturn true />
<cfelseif arguments.currentTotal gt 15.05>
<cfoutput>#arguments.currentCombo# > 15.05 (aborting)</cfoutput><br />
<cfreturn false />
<cfelse>
<!--- less than 15.05 --->
<cfoutput>#arguments.currentCombo# < 15.05 (traversing)</cfoutput><br />
<cfset found = testCombo(arguments.currentCombo, arguments.currentTotal, arguments.apps) />
</cfif>
</cfloop>
</cffunction>
<cfset mf = {name="Mixed Fruit", cost=2.15} />
<cfset ff = {name="French Fries", cost=2.75} />
<cfset ss = {name="side salad", cost=3.35} />
<cfset hw = {name="hot wings", cost=3.55} />
<cfset ms = {name="moz sticks", cost=4.20} />
<cfset sp = {name="sampler plate", cost=5.80} />
<cfset apps = [ mf, ff, ss, hw, ms, sp ] />
<cfloop from="1" to="6" index="b">
<cfoutput>#testCombo(apps[b].name, apps[b].cost, apps)#</cfoutput>
</cfloop>
위의 코드는 최대 $ 15.05를 추가하는 유일한 조합은 7 주문의 혼합 과일이며 232 개의 TestCombo 기능을 수행하는 데 232 개의 실행이 필요하다는 것을 알려줍니다.
올바른 솔루션에 도달하기에 더 나은 알고리즘이 있습니까? 내가 올바른 해결책을 찾았습니까?
해결책
NP- 완료 문제에 대한 요점은 소규모 데이터 세트에서 까다로운 것이 아니라 해결하기위한 작업량이 다항식보다 더 큰 속도로 성장한다는 것입니다. 즉, O (n^x) 알고리즘이 없습니다.
시간 복잡성이 O (n!) 인 경우 위에서 언급 한 두 가지 문제는 NP에 있습니다.
다른 팁
솔루션의 모든 순열을 제공하지만 코드 크기로 다른 모든 사람들을 때리고 있다고 생각합니다.
item(X) :- member(X,[215, 275, 335, 355, 420, 580]).
solution([X|Y], Z) :- item(X), plus(S, X, Z), Z >= 0, solution(Y, S).
solution([], 0).
Swiprolog를 사용한 솔루션 :
?- solution(X, 1505).
X = [215, 215, 215, 215, 215, 215, 215] ;
X = [215, 355, 355, 580] ;
X = [215, 355, 580, 355] ;
X = [215, 580, 355, 355] ;
X = [355, 215, 355, 580] ;
X = [355, 215, 580, 355] ;
X = [355, 355, 215, 580] ;
X = [355, 355, 580, 215] ;
X = [355, 580, 215, 355] ;
X = [355, 580, 355, 215] ;
X = [580, 215, 355, 355] ;
X = [580, 355, 215, 355] ;
X = [580, 355, 355, 215] ;
No
Isn't it more elegant with recursion (in Perl)?
#!/usr/bin/perl
use strict;
use warnings;
my @weights = (2.15, 2.75, 3.35, 3.55, 4.20, 5.80);
my $total = 0;
my @order = ();
iterate($total, @order);
sub iterate
{
my ($total, @order) = @_;
foreach my $w (@weights)
{
if ($total+$w == 15.05)
{
print join (', ', (@order, $w)), "\n";
}
if ($total+$w < 15.05)
{
iterate($total+$w, (@order, $w));
}
}
}
Output
marco@unimatrix-01:~$ ./xkcd-knapsack.pl
2.15, 2.15, 2.15, 2.15, 2.15, 2.15, 2.15
2.15, 3.55, 3.55, 5.8
2.15, 3.55, 5.8, 3.55
2.15, 5.8, 3.55, 3.55
3.55, 2.15, 3.55, 5.8
3.55, 2.15, 5.8, 3.55
3.55, 3.55, 2.15, 5.8
3.55, 5.8, 2.15, 3.55
5.8, 2.15, 3.55, 3.55
5.8, 3.55, 2.15, 3.55
Even though knapsack is NP Complete, it is a very special problem: the usual dynamic program for it is in fact excellent (http://en.wikipedia.org/wiki/Knapsack_problem)
And if you do the correct analysis, it turns out that it is O(nW), n being the # of items, and W being the target number. The problem is when you have to DP over a large W, that's when we get the NP behaviour. But for the most part, knapsack is reasonably well behaved and you can solve really large instances of it with no problems. As far as NP complete problems go, knapsack is one of the easiest.
Here is the solution using constraint.py
>>> from constraint import *
>>> problem = Problem()
>>> menu = {'mixed-fruit': 2.15,
... 'french-fries': 2.75,
... 'side-salad': 3.35,
... 'hot-wings': 3.55,
... 'mozarella-sticks': 4.20,
... 'sampler-plate': 5.80}
>>> for appetizer in menu:
... problem.addVariable( appetizer, [ menu[appetizer] * i for i in range( 8 )] )
>>> problem.addConstraint(ExactSumConstraint(15.05))
>>> problem.getSolutions()
[{'side-salad': 0.0, 'french-fries': 0.0, 'sampler-plate': 5.7999999999999998, 'mixed-fruit': 2.1499999999999999, 'mozarella-sticks': 0.0, 'hot-wings': 7.0999999999999996},
{'side-salad': 0.0, 'french-fries': 0.0, 'sampler-plate': 0.0, 'mixed-fruit': 15.049999999999999, 'mozarella-sticks': 0.0, 'hot-wings': 0.0}]
So the solution is to order a sampler plate, a mixed fruit, and 2 orders of hot wings, or order 7 mixed-fruits.
Here's a solution with F#:
#light
type Appetizer = { name : string; cost : int }
let menu = [
{name="fruit"; cost=215}
{name="fries"; cost=275}
{name="salad"; cost=335}
{name="wings"; cost=355}
{name="moz sticks"; cost=420}
{name="sampler"; cost=580}
]
// Choose: list<Appetizer> -> list<Appetizer> -> int -> list<list<Appetizer>>
let rec Choose allowedMenu pickedSoFar remainingMoney =
if remainingMoney = 0 then
// solved it, return this solution
[ pickedSoFar ]
else
// there's more to spend
[match allowedMenu with
| [] -> yield! [] // no more items to choose, no solutions this branch
| item :: rest ->
if item.cost <= remainingMoney then
// if first allowed is within budget, pick it and recurse
yield! Choose allowedMenu (item :: pickedSoFar) (remainingMoney - item.cost)
// regardless, also skip ever picking more of that first item and recurse
yield! Choose rest pickedSoFar remainingMoney]
let solutions = Choose menu [] 1505
printfn "%d solutions:" solutions.Length
solutions |> List.iter (fun solution ->
solution |> List.iter (fun item -> printf "%s, " item.name)
printfn ""
)
(*
2 solutions:
fruit, fruit, fruit, fruit, fruit, fruit, fruit,
sampler, wings, wings, fruit,
*)
Read up on the Knapsack Problem.
You've got all the correct combinations now, but you're still checking many more than you need to (as evidenced by the many permutations your result shows). Also, you're omitting the last item that hits the 15.05 mark.
I have a PHP version that does 209 iterations of the recursive call (it does 2012 if I get all permutations). You can reduce your count if right before the end of your loop, you pull out the item you just checked.
I don't know CF syntax, but it will be something like this:
<cfelse>
<!--- less than 15.50 --->
<!--<cfoutput>#arguments.currentCombo# < 15.05 (traversing)</cfoutput><br />-->
<cfset found = testCombo(CC, CT, arguments.apps) />
------- remove the item from the apps array that was just checked here ------
</cfif>
</cfloop>
EDIT: For reference, here's my PHP version:
<?
function rc($total, $string, $m) {
global $c;
$m2 = $m;
$c++;
foreach($m as $i=>$p) {
if ($total-$p == 0) {
print "$string $i\n";
return;
}
if ($total-$p > 0) {
rc($total-$p, $string . " " . $i, $m2);
}
unset($m2[$i]);
}
}
$c = 0;
$m = array("mf"=>215, "ff"=>275, "ss"=>335, "hw"=>355, "ms"=>420, "sp"=>580);
rc(1505, "", $m);
print $c;
?>
Output
mf mf mf mf mf mf mf
mf hw hw sp
209
EDIT 2:
Since explaining why you can remove the elements will take a little more than I could fit in a comment, I'm adding it here.
Basically, each recursion will find all combinations that include the currently search element (e.g., the first step will find everything including at least one mixed fruit). The easiest way to understand it is to trace the execution, but since that will take a lot of space, I'll do it as if the target was 6.45.
MF (2.15)
MF (4.30)
MF (6.45) *
FF (7.05) X
SS (7.65) X
...
[MF removed for depth 2]
FF (4.90)
[checking MF now would be redundant since we checked MF/MF/FF previously]
FF (7.65) X
...
[FF removed for depth 2]
SS (5.50)
...
[MF removed for depth 1]
At this point, we've checked every combination that includes any mixed fruit, so there's no need to check for mixed fruit again. You can use the same logic to prune the array at each of the deeper recursions as well.
Tracing through it like this actually suggested another slight time saver -- knowing the prices are sorted from low to high means that we don't need to keep checking items once we go over the target.
I would make one suggestion about the design of the algorithm itself (which is how I interpreted the intent of your original question). Here is a fragment of the solution I wrote:
....
private void findAndReportSolutions(
int target, // goal to be achieved
int balance, // amount of goal remaining
int index // menu item to try next
) {
++calls;
if (balance == 0) {
reportSolution(target);
return; // no addition to perfect order is possible
}
if (index == items.length) {
++falls;
return; // ran out of menu items without finding solution
}
final int price = items[index].price;
if (balance < price) {
return; // all remaining items cost too much
}
int maxCount = balance / price; // max uses for this item
for (int n = maxCount; 0 <= n; --n) { // loop for this item, recur for others
++loops;
counts[index] = n;
findAndReportSolutions(
target, balance - n * price, index + 1
);
}
}
public void reportSolutionsFor(int target) {
counts = new int[items.length];
calls = loops = falls = 0;
findAndReportSolutions(target, target, 0);
ps.printf("%d calls, %d loops, %d falls%n", calls, loops, falls);
}
public static void main(String[] args) {
MenuItem[] items = {
new MenuItem("mixed fruit", 215),
new MenuItem("french fries", 275),
new MenuItem("side salad", 335),
new MenuItem("hot wings", 355),
new MenuItem("mozzarella sticks", 420),
new MenuItem("sampler plate", 580),
};
Solver solver = new Solver(items);
solver.reportSolutionsFor(1505);
}
...
(Note that the constructor does sort the menu items by increasing price, to enable the constant-time early termination when the remaining balance is smaller than any remaining menu item.)
The output for a sample run is:
7 mixed fruit (1505) = 1505
1 mixed fruit (215) + 2 hot wings (710) + 1 sampler plate (580) = 1505
348 calls, 347 loops, 79 falls
The design suggestion I want to highlight is that in the above code, each nested (recursive) call of findAndReportSolution(...) deals with the quantity of exactly one menu item, identified by the index argument. In other words, the recursive nesting parallels the behavior of an in-line set of nested loops; the outermost counts possible uses of the first menu item, the next in counts the uses of the second menu item, etc. (Except, of course, the use of recursion liberates the code from dependence on a specific number of menu items!)
I suggest that this makes it easier to design the code, and easier to understand what each invocation is doing (accounting for all possible uses of a specific item, delegating the remainder of the menu to subordinate calls). It also avoids the combinatorial explosion of producing all arrangements of a multiple-item solution (as in the second line of the above output, which only occurs once, instead of repeatedly with different orderings of the items).
I try to maximize the "obviousness" of the code, rather than trying to minimize the number of calls of some specific method. For example, the above design lets a delegated call determine if a solution has been reached, rather than wrapping that check around the point of the call, which would reduce the number of calls at the expense of cluttering up the code.
Hmm, you know what's weird. The solution is seven of the first item on the menu.
Since this was obviously meant to be solved by paper and pencil in a short time frame, why not divide the order total by the price of each item to see if by some chance they ordered multiples of one item?
For example,
15.05/2.15 = 7 mixed fruits 15.05/2.75 = 5.5 french fries.
And then move on to simple combinations...
15 / (2.15 + 2.75) = 3.06122449 mixed fruits with french fries.
In other words, assume that the solution is supposed to be simple and solvable by a human without access to a computer. Then test if the simplest, most obvious (and therefore hidden in plain sight) solution(s) work(s).
I swear I'm pulling this at the local coney this weekend when I order $4.77 worth of appetizers (including tax) at 4:30 AM after the club closes.
In python.
I had some problems with "global vars" so I put the function as method of an object. It is recursive and it calls itself 29 times for the question in the comic, stopping at the first successful match
class Solver(object):
def __init__(self):
self.solved = False
self.total = 0
def solve(s, p, pl, curList = []):
poss = [i for i in sorted(pl, reverse = True) if i <= p]
if len(poss) == 0 or s.solved:
s.total += 1
return curList
if abs(poss[0]-p) < 0.00001:
s.solved = True # Solved it!!!
s.total += 1
return curList + [poss[0]]
ml,md = [], 10**8
for j in [s.solve(p-i, pl, [i]) for i in poss]:
if abs(sum(j)-p)<md: ml,md = j, abs(sum(j)-p)
s.total += 1
return ml + curList
priceList = [5.8, 4.2, 3.55, 3.35, 2.75, 2.15]
appetizers = ['Sampler Plate', 'Mozzarella Sticks', \
'Hot wings', 'Side salad', 'French Fries', 'Mixed Fruit']
menu = zip(priceList, appetizers)
sol = Solver()
q = sol.solve(15.05, priceList)
print 'Total time it runned: ', sol.total
print '-'*30
order = [(m, q.count(m[0])) for m in menu if m[0] in q]
for o in order:
print '%d x %s \t\t\t (%.2f)' % (o[1],o[0][1],o[0][0])
print '-'*30
ts = 'Total: %.2f' % sum(q)
print ' '*(30-len(ts)-1),ts
Output:
Total time it runned: 29
------------------------------
1 x Sampler Plate (5.80)
2 x Hot wings (3.55)
1 x Mixed Fruit (2.15)
------------------------------
Total: 15.05
Actually, I've refactored my algorithm some more. There were several correct combinations I was missing, and it was due to the fact that I was returning as soon as the cost went over 15.05 -- I wasn't bothering to check other (cheaper) items that I could add. Here's my new algorithm:
<cffunction name="testCombo" returntype="numeric">
<cfargument name="currentCombo" type="string" required="true" />
<cfargument name="currentTotal" type="numeric" required="true" />
<cfargument name="apps" type="array" required="true" />
<cfset var a = 0 />
<cfset var found = false />
<cfset var CC = "" />
<cfset var CT = 0 />
<cfset tries = tries + 1 />
<cfloop from="1" to="#arrayLen(arguments.apps)#" index="a">
<cfset combos = combos + 1 />
<cfset CC = listAppend(arguments.currentCombo, arguments.apps[a].name) />
<cfset CT = arguments.currentTotal + arguments.apps[a].cost />
<cfif CT eq 15.05>
<!--- print current combo --->
<cfoutput><strong>#CC# = 15.05</strong></cfoutput><br />
<cfreturn true />
<cfelseif CT gt 15.05>
<!--<cfoutput>#arguments.currentCombo# > 15.05 (aborting)</cfoutput><br />-->
<cfelse>
<!--- less than 15.50 --->
<!--<cfoutput>#arguments.currentCombo# < 15.05 (traversing)</cfoutput><br />-->
<cfset found = testCombo(CC, CT, arguments.apps) />
</cfif>
</cfloop>
<cfreturn found />
</cffunction>
<cfset mf = {name="Mixed Fruit", cost=2.15} />
<cfset ff = {name="French Fries", cost=2.75} />
<cfset ss = {name="side salad", cost=3.35} />
<cfset hw = {name="hot wings", cost=3.55} />
<cfset ms = {name="moz sticks", cost=4.20} />
<cfset sp = {name="sampler plate", cost=5.80} />
<cfset apps = [ mf, ff, ss, hw, ms, sp ] />
<cfset tries = 0 />
<cfset combos = 0 />
<cfoutput>
<cfloop from="1" to="6" index="b">
#testCombo(apps[b].name, apps[b].cost, apps)#
</cfloop>
<br />
tries: #tries#<br />
combos: #combos#
</cfoutput>
Output:
Mixed Fruit,Mixed Fruit,Mixed Fruit,Mixed Fruit,Mixed Fruit,Mixed Fruit,Mixed Fruit = 15.05
Mixed Fruit,hot wings,hot wings,sampler plate = 15.05
Mixed Fruit,hot wings,sampler plate,hot wings = 15.05
Mixed Fruit,sampler plate,hot wings,hot wings = 15.05
false false false hot wings,Mixed Fruit,hot wings,sampler plate = 15.05
hot wings,Mixed Fruit,sampler plate,hot wings = 15.05
hot wings,hot wings,Mixed Fruit,sampler plate = 15.05
hot wings,sampler plate,Mixed Fruit,hot wings = 15.05
false false sampler plate,Mixed Fruit,hot wings,hot wings = 15.05
sampler plate,hot wings,Mixed Fruit,hot wings = 15.05
false
tries: 2014
combos: 12067
I think this may have all of the correct combinations, but my question still stands: Is there a better algorithm?
Learning from @rcar's answer, and another refactoring later, I've got the following.
As with so many things I code, I've refactored from CFML to CFScript, but the code is basically the same.
I added in his suggestion of a dynamic start point in the array (instead of passing the array by value and changing its value for future recursions), which brought me to the same stats he gets (209 recursions, 571 combination price checks (loop iterations)), and then improved on that by assuming that the array will be sorted by cost -- because it is -- and breaking as soon as we go over the target price. With the break, we're down to 209 recursions and 376 loop iterations.
What other improvements could be made to the algorithm?
function testCombo(minIndex, currentCombo, currentTotal){
var a = 0;
var CC = "";
var CT = 0;
var found = false;
tries += 1;
for (a=arguments.minIndex; a <= arrayLen(apps); a++){
combos += 1;
CC = listAppend(arguments.currentCombo, apps[a].name);
CT = arguments.currentTotal + apps[a].cost;
if (CT eq 15.05){
//print current combo
WriteOutput("<strong>#CC# = 15.05</strong><br />");
return(true);
}else if (CT gt 15.05){
//since we know the array is sorted by cost (asc),
//and we've already gone over the price limit,
//we can ignore anything else in the array
break;
}else{
//less than 15.50, try adding something else
found = testCombo(a, CC, CT);
}
}
return(found);
}
mf = {name="mixed fruit", cost=2.15};
ff = {name="french fries", cost=2.75};
ss = {name="side salad", cost=3.35};
hw = {name="hot wings", cost=3.55};
ms = {name="mozarella sticks", cost=4.20};
sp = {name="sampler plate", cost=5.80};
apps = [ mf, ff, ss, hw, ms, sp ];
tries = 0;
combos = 0;
testCombo(1, "", 0);
WriteOutput("<br />tries: #tries#<br />combos: #combos#");
Here's concurrent implementation in Clojure. To calculate (items-with-price 15.05) takes about 14 combination-generation recursions, and about 10 possibility-checks. Took me about 6 minutes to calculate (items-with-price 100) on my Intel Q9300.
This only gives the first found answer, or nil if there is none, as that's all the problem calls for. Why do more work that you've been told to do ;) ?
;; np-complete.clj
;; A Clojure solution to XKCD #287 "NP-Complete"
;; By Sam Fredrickson
;;
;; The function "items-with-price" returns a sequence of items whose sum price
;; is equal to the given price, or nil.
(defstruct item :name :price)
(def *items* #{(struct item "Mixed Fruit" 2.15)
(struct item "French Fries" 2.75)
(struct item "Side Salad" 3.35)
(struct item "Hot Wings" 3.55)
(struct item "Mozzarella Sticks" 4.20)
(struct item "Sampler Plate" 5.80)})
(defn items-with-price [price]
(let [check-count (atom 0)
recur-count (atom 0)
result (atom nil)
checker (agent nil)
; gets the total price of a seq of items.
items-price (fn [items] (apply + (map #(:price %) items)))
; checks if the price of the seq of items matches the sought price.
; if so, it changes the result atom. if the result atom is already
; non-nil, nothing is done.
check-items (fn [unused items]
(swap! check-count inc)
(if (and (nil? @result)
(= (items-price items) price))
(reset! result items)))
; lazily generates a list of combinations of the given seq s.
; haven't tested well...
combinations (fn combinations [cur s]
(swap! recur-count inc)
(if (or (empty? s)
(> (items-price cur) price))
'()
(cons cur
(lazy-cat (combinations (cons (first s) cur) s)
(combinations (cons (first s) cur) (rest s))
(combinations cur (rest s))))))]
; loops through the combinations of items, checking each one in a thread
; pool until there are no more combinations or the result atom is non-nil.
(loop [items-comb (combinations '() (seq *items*))]
(if (and (nil? @result)
(not-empty items-comb))
(do (send checker check-items (first items-comb))
(recur (rest items-comb)))))
(await checker)
(println "No. of recursions:" @recur-count)
(println "No. of checks:" @check-count)
@result))
If you want an optimized algorithm, it's best to try the prices in descending order. That lets you use up as much of the remaining amount first and then see how the rest can be filled in.
Also, you can use math to figure out the maximum quantity of each food item to start each time so you don't try combinations that would go over the $15.05 goal.
This algorithm only needs to try 88 combinations to get a complete answer and that looks like the lowest that's been posted so far:
public class NPComplete {
private static final int[] FOOD = { 580, 420, 355, 335, 275, 215 };
private static int tries;
public static void main(String[] ignore) {
tries = 0;
addFood(1505, "", 0);
System.out.println("Combinations tried: " + tries);
}
private static void addFood(int goal, String result, int index) {
// If no more food to add, see if this is a solution
if (index >= FOOD.length) {
tries++;
if (goal == 0)
System.out.println(tries + " tries: " + result.substring(3));
return;
}
// Try all possible quantities of this food
// If this is the last food item, only try the max quantity
int qty = goal / FOOD[index];
do {
addFood(goal - qty * FOOD[index],
result + " + " + qty + " * " + FOOD[index], index + 1);
} while (index < FOOD.length - 1 && --qty >= 0);
}
}
Here's the output showing the two solutions:
9 tries: 1 * 580 + 0 * 420 + 2 * 355 + 0 * 335 + 0 * 275 + 1 * 215 88 tries: 0 * 580 + 0 * 420 + 0 * 355 + 0 * 335 + 0 * 275 + 7 * 215 Combinations tried: 88