Trouver si un angle est à X degrés d'une autre

Question

J'ai besoin d'un algorithme pour déterminer si un angle est dans une certaine quantité de degrés sous un autre angle.

Ma première pensée était (a-x < b) && (a+x > b), mais il échoue quand il doit travailler avec des angles qui enveloppent -179 à 180.

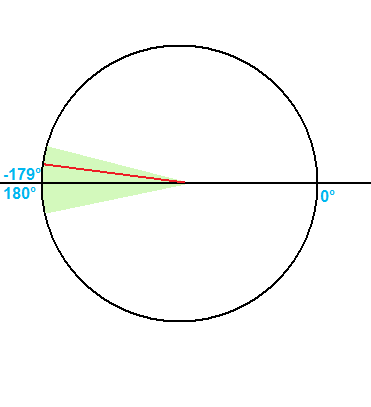
Dans le schéma ci-dessus, la région (vert) que l'angle doit être compris entre des enveloppes entre les côtés négatif et positif. Comment puis-je déterminer si l'angle (la ligne rouge) tombe dans cette région?

Answer 1

essayer cette formule:

360-(|a-b|)%360<x || (|a-b|)%360<x

Ou, en PHP :

<?php

$b = 10;
$angle1 = -179;
$angle2 = 180;

$diff = $angle1 - $angle2;
if(abs($diff % 360) <= $b || (360-abs($diff % 360))<=$b) {
  echo "yes";
} else {
  echo "no";
}

?>

Answer 2

Comme Marcel souligne à juste titre, modulo sur les nombres négatifs est potentiellement problématique. De plus, quelle est la différence entre 355 et 5 degrés? Il pourrait être élaboré à 350 degrés, mais 10 degrés est probablement ce que les gens attendent. Nous faisons les hypothèses suivantes:

1. nous voulons que le plus petit angle positif entre deux autres angles si 0 <= diff <= 180;
2. nous travaillons en degrés. Si radians, remplacer 360 pour 2*PI;
3. angles peuvent être positives ou négatives peuvent être en dehors de la gamme -360 < x < 360 où x est un angle d'entrée et
4. ordre d'angles d'entrée ou de la direction de la différence est sans importance.

Entrées: les angles a et b. Ainsi, l'algorithme est simplement:

1. Normaliser a et b pour 0 <= x < 360;
2. Calculer l'angle le plus court entre les deux angles normaux.

Pour la première étape, pour convertir l'angle de la gamme désirée, il existe deux possibilités:

• x >= 0: normal = x% 360
• x < 0: normal = (-x / 360 + 1) * 360 + x

Le second est conçu pour lever toute ambiguïté sur la différence dans l'interprétation des opérations de module négatives. Donc, pour donner un exemple travaillé pour x = -400:

  -x / 360 + 1
= -(-400) / 360 + 1
= 400 / 360 + 1
= 1 + 1
= 2

puis

normal = 2 * 360 + (-400)
       = 320

so pour les entrées 10 et -400 les angles normaux sont de 10 et 320.

Maintenant, on calcule l'angle le plus court entre eux. Comme un contrôle de santé mentale, la somme de ces deux angles doit être 360. Dans ce cas, les possibilités sont 50 et 310 (dessiner et vous verrez cela). Pour ceux-ci sur:

normal1 = min(normal(a), normal(b))
normal2 = max(normal(a), normal(b))
angle1 = normal2 - normal1
angle2 = 360 + normal1 - normal2

Donc, pour notre exemple:

normal1 = min(320, 10) = 10
normal2 = max(320, 10) = 320
angle1 = normal2 - normal1 = 320 - 10 = 310
angle2 = 360 + normal1 - normal2 = 360 + 10 - 320 = 50

Vous remarquerez normal1 + normal2 = 360 (et vous pouvez même prouver que ce sera le cas si vous le souhaitez).

Enfin:

diff = min(normal1, normal2)

ou 50 dans notre cas.

Answer 3

Pour un rayon de 1, la distance entre les points de terminaison de ligne est 2sin ((ab / 2). Donc, jeter le 2 puisque vous êtes seulement intéressé par une comparaison, et comparer sin (x / 2) avec le péché (( ab) / 2). les fonctions trigonométriques prendre soin de tout l'emballage.

Answer 4

Vous pouvez également utiliser un produit scalaire:

cos(a)*cos(b) + sin(a)*sin(b) >= cos(x)

Answer 5

c ++ mise en œuvre:

float diff = fabsf(angle1 - angle2);
bool isInRange = fmodf(diff, 360.0f) <= ANGLE_RANGE ||
                 360.0f - fmodf(diff, 360.0f) <= ANGLE_RANGE;